قانون سینوس ها ، رابطهای است که کاربرد بسیاری در محاسبات مربوط به مثلثها دارد. البته جهت تحلیل زوایا و اندازه اضلاع یک مثلث میتوان از قانون کسینوسها نیز بهره برد. در این آموزش قصد داریم تا با مثالهای کاربردی، قانون سینوس ها را یاد بگیریم.
جهت بیان این قانون، در ابتدا مثلث زیر را در نظر بگیرید.
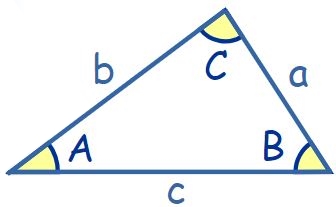
همانطور که در مثلث فوق نشان داده شده، حروف کوچک بیانکننده اضلاع و حروف بزرگ بیانکننده زوایای مثلث هستند. قانون سینوسها، رابطه زیر را بین طول اضلاع و زوایا، به شکل زیر بیان میکند:
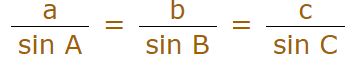
در حقیقت رابطه بالا بیان میکند که حاصل تقسیم یک ضلع مثلث به سینوس زاویه مقابلش، برای تمامی اضلاع آن، مقداری ثابت است. جهت آزمایش این رابطه، مثلثی مطابق با تصویر زیر با زوایا و طولهای مشخصی رسم شده است.
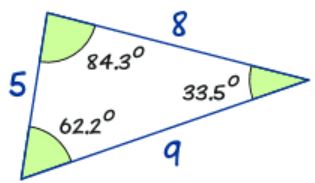
حاصل تقسیم هر ضلع به سینوس زاویه مقابلش برابر است با:

همانطور که در بالا نیز محاسبه شد، حاصل عبارات بدست آمده، تقریبا با یکدیگر برابر هستند.
بکارگیری این قانون
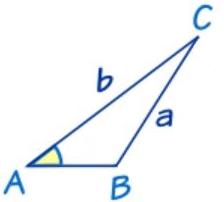
این قانون در تحلیل هندسی مسائل بسیار کاربرد دارد. در حقیقت میتوان با استفاده از آن اضلاع و یا زوایای مجهول را در یک مثلث یافت. جهت نحوه استفاده از این قانون، به نمونههایی که در ادامه آمده، توجه فرمایید. در ابتدا مثلثی را مطابق با شکل زیر در نظر بگیرید.
پیدا کردن اندازه ضلع
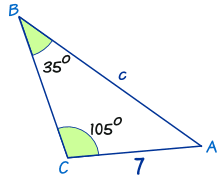
به نظر شما اندازه ضلع c چقدر است؟ جهت پاسخ به این سوال، قانون سینوسها را به شکل زیر مینویسیم.

با برابر قرار دادن عبارت دوم و سوم رابطه بالا، داریم:
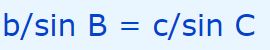
پس از جایگذاری مقادیر معلوم در رابطه بالا:
![]()
با حل معادله خطی بالا داریم:

پیدا کردن زاویه مجهول
در مثال بالا، اندازه ضلع مجهول یافت شد. حال مطابق با شکل زیر مثلثی را در نظر بگیرید که در آن دو زاویه مجهول (A و B) وجود دارد. فرض کنید هدف ما محاسبه زاویه B باشد.
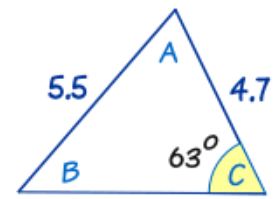
به ترتیب زیر میتوان زاویه B را بدست آورد:
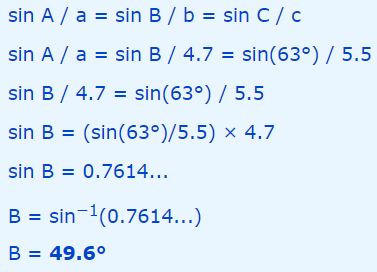
دو پاسخ برای قانون سینوس ها
در برخی از مواقع، با نوشتن قانون سینوس ها ، به دو پاسخ برای اضلاع و یا زاویهها میرسیم. برای نمونه مطابق با شکل زیر، مثلثی را با زاویه A و طول اضلاع a و b تصور کنید.
میتوان با ثابت نگه داشتن زاویه A و ضلع b، ظلع a را دوران داده به به مثلثی با همین مشخصات دست یافت. همانگونه که در شکل زیر میبینید ظلع a دوران یافته و مثلث مشابهی را بهوجود آورده که در آن مقادیر A ،a ،b برابر با مثلث بالا است.
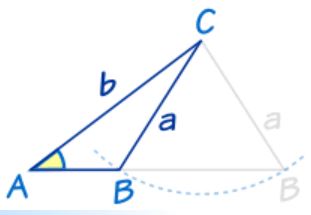
در حالتی این اتفاق میافتد که دو ضلع و زاویه خارج از آنها معلوم باشد. اگر زاویه معلوم، بین دو ضلع باشد، در این صورت تنها یک مثلث وجود خواهد داشت. برای درک بهتر به مثال زیر توجه کنید.
زاویه R را در مثلث زیر بیابید.
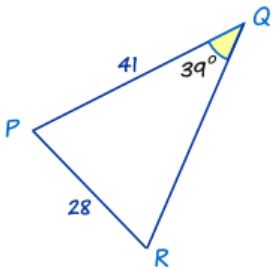
با توجه به مشخصات ارائه شده در شکل بالا، قانون سینوس ها را میتوان بهترتیب زیر بیان کرد:
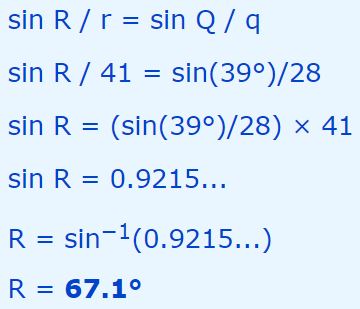
به نظر شما ابهام در پاسخ بالا در کدام عبارت نهفته است. در حقیقت با تفکر در روش بالا متوجه میشویم که (R = sin-1 (0.9215 دارای دو پاسخ است. در حقیقت زاویهای دیگر به جز ۶۷.۱ درجه وجود دارد که سینوس آن نیز برابر با ۰.۹۲۱۵ است. این زاویه برابر با مقدار زیر است:
![]()
بنابراین با ثوابت مطرح شده در صورت سوال، دو مثلث زیر را میتوان رسم کرد:
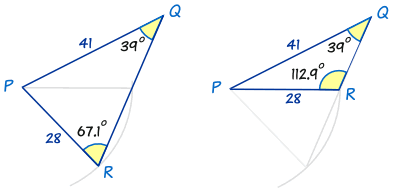
در هر دو مثلث بالا زاویه ۳۹ درجه و دو ظلع با طولهای ۴۱ و ۲۸ وجود دارد! بهیاد داشته باشید که همواره بایستی پاسخ دوم را از نظر منطقی چک کرد.
منبع:فرادرس


بدون دیدگاه