در گذشته مطالبی مطرح شد که با مفهوم سینوس و کسینوس و تانژانت به زبان ساده آشنا شدیم و در این مطلب درباره مفهوم توابع معکوس مثلثاتی و بطور مثال آرک تانژانت چیست صحبت خواهیم کرد.
مفهوم توابع معکوس مثلثاتی
همانطور که پیشتر نیز بیان شد، سینوس و کسینوس و تانژانت زاویه، مفاهیمی هستند که با استفاده از آنها میتوان بین طول و زوایای یک مثلث ارتباط برقرار کرد. در ابتدا شکل زیر را در نظر بگیرید.
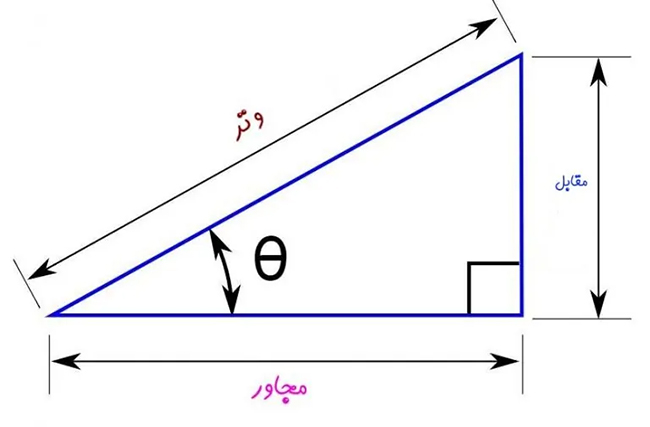
با توجه به شکل فوق، مقادیر مثلثاتی به صورت زیر تعریف میشوند:

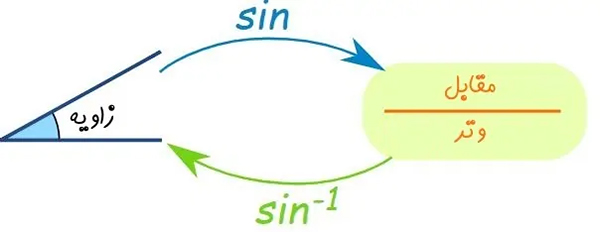
بنابراین یک زاویه در سینوس یا کسینوس قرار داده شده و خروجی آن محاسبه میشود. حال اگر مقدار خروجی را داشته باشیم با استفاده از تابع سینوس معکوس یا آرک سینوس، مقدار زاویهی متناسب با آن بدست میآید.
بنابراین تابع ورودی را گرفته و خروجی آن نسبت طول اضلاع میشود. حال تابع خروجی را میگیرد و به ما زاویه میدهد.
مثال 1:
مقدار را بیابید.
برای بدست آوردن این مقدار، باید نگاه کنیم و ببینیم سینوس چه زاویهای برابر با ۰.۵۷ میشود. با استفاده از ماشین حساب میتوان دید سینوس زاویه ۳۵ درجه برابر با ۰.۵۷ است. بنابراین میتوان گفت:
sin–1(0.57)=35o
توجه داشته باشید که توابع معکوس مثلثاتی را ممکن است به صورت آرک نیز نشان دهند. در ادامه این شکل از تابع معکوس نشان داده شده است.
احتمالا تاکنون متوجه شدهاید که بیانهای زیر معادل یکدیگر هستند.
θ=cos–1(x)⇔x=cos(θ)
θ=sin–1(x)⇔x=sin(θ)
θ=tan–1(x)⇔x=tan(θ)
مثال 2:
مقدار را بدست آورید.
در ابتدا دایره مثلثاتی را به صورت زیر ترسیم کنید.
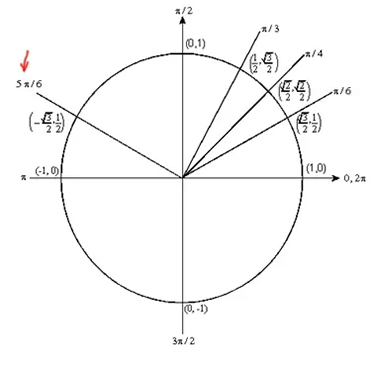
با توجه به دایره، مقدار کسینوس معکوس یا آرک کسینوس برابر میشود با:
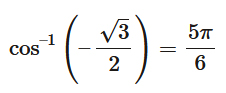
نمودار توابع معکوس مثلثاتی
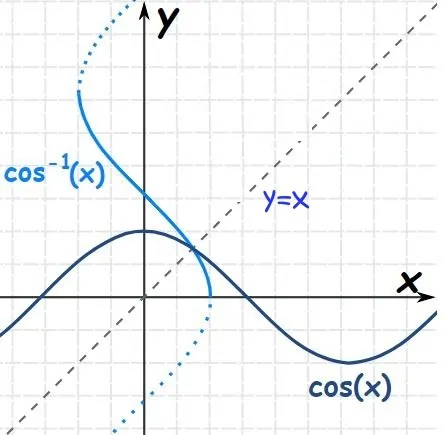
در مثال ۱ توابع معکوس مثلثاتی از جمله ارک تانژانت ارائه شدند. برای بدست آوردن نمودار توابع معکوس کافی است که آنها را نسبت به محور y=x معکوس کنیم. برای نمونه در شکل زیر نمودار تابع y=cos x نسبت به y=x قرینه شده و تابع y=cos-1x بدست آمده است.
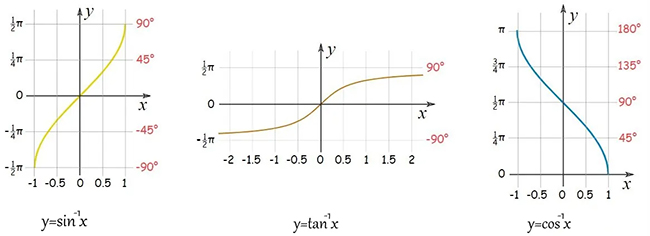
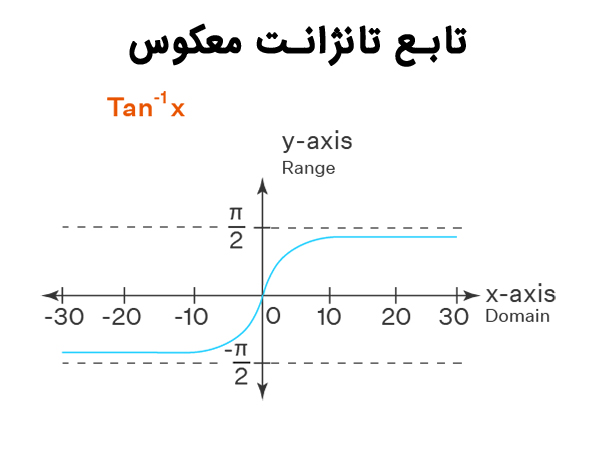
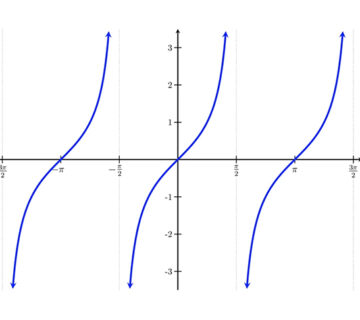
در ادامه نمودار توابع ارک سینوس و ارک کسینوس و ارک تانژانت ارائه شده است.


بدون دیدگاه