ماتریس چیست به زبان ساده
ماتریس، آرایشی منظم از اعداد است که در سطر و ستونهای مشخصی مرتب شدهاند. برای مثال در تصویر زیر یک ماتریس با 2 سطر و 3 ستون مشاهده میکنید که ماتریس 3×2 نامیده میشود:
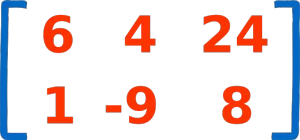
کاربرد ماتریس چیست؟ ماتریسها کاربردهای زیادی در محاسبات شاخههای مختلف دانش دارند و در واقع کارهای بسیاری را می شود با ماتریس ها انجام داد. برای نمونه میتوان با استفاده از آنها معادلات با درجه ۳، ۴ و بالاتر را تحلیل و پاسخهای آنها را بدست آورد. ماتریسها اغلب در زمینه های علمی مانند فیزیک، گرافیک کامپیوتری، نظریه احتمالات، آمار، حساب دیفرانسیل و انتگرال، آنالیز عددی و غیره استفاده می شوند.
سطر ها و ستون های ماتریس
هر ماتریس از یک یا چند سطر و ستون تشکیل یافته است.
- سطر ها از چپ به راست هستند.
- ستون ها از بالا به پایین هستند.
باید توجه داشته باشید که در هر عملیاتی بر روی ماتریس، سطرها بر ستونها مقدم هستند.
درایه
ماتریس معمولا با یک حرف بزرگ انگلیسی (مانند A یا B) نمایش داده می شود. به هر یک از اعداد درون ماتریس یک عنصر یا درایه ماتریس گفته می شود. برای مشخص کردن هر درایه در ماتریس عدد ردیف و ستون آن را به ترتیب بصورت زیرنویس حرف کوچک نام ماتریس می نویسیم. برای نمونه اگر یک ماتریس A نام دارد، درایه ای که در سطر دوم و ستون سوم آن قرار دارد به صورت a23 مشخص میشود.

برخی از درایه های نمونه عبارتند از:
- b1,1 = 6 (درایه ماتریس در سطر 1 و ستون 1 برابر 6 است)
- b1,3 = 24 (درایه ماتریس در سطر 1 و ستون 3 برابر 24 است)
- b2,3 = 8 (درایه ماتریس در سطر 2 و ستون 3 برابر 8 است)
مرتبه ماتریس
به تعداد سطرها و ستونهای ماتریس که به صورت (ستون×سطر) نوشته میشود، مرتبه ماتریس می گوییم. برای مثال مرتبه ماتریس تصویر فوق 3×2 است و می گوییم این یک ماتریس 2 در 3 است. ماتریسی که تنها یک سطر داشته باشد، ماتریس سطری و ماتریسی که تنها یک ستون داشته باشد، ماتریس ستونی نامیده میشود. البته ماتریس تهی هم داریم، که ماتریسی است که هیچ درایهای ندارد. به ماتریسی که تعداد سطر ها و ستونهایش برابر باشند ماتریس مربعی گفته می شود.
باتوجه به محدودیت ابعاد این صفحه برای محاسبه ماتریس با مرتبه بیشتر از 5×5 تا 10×10 از لینک زیر استفاده فرمایید.
عملیات ماتریسها
در ادامه به انواع مختلف عملیات ریاضی در مورد ماتریسها می پردازیم.
جمع ماتریسها
برای جمع دو ماتریس، اعداد هم مرتبه آنها را با هم جمع کنید:
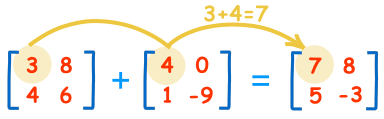
مثال: یک ماتریس با 3 سطر و 5 ستون می تواند با یک ماتریس دیگر که 3 سطر و 5 ستون دارد جمع شود؛ اما این ماتریس نمی تواند با یک ماتریس که 3 سطر و 4 ستون دارد جمع شود؛ چون اندازه ستون ها برابر نیست.
تفریق ماتریسها
برای تفریق دو ماتریس می بایست اعداد هم مرتبه ماتریس ها را از هم تفریق کنید:
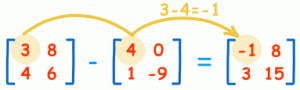
دترمینان ماتریس
دترمینان (Determinant) ماتریس، عدد مخصوصی است که برای ماتریسهای مربع محاسبه می شود.
دترمینان اطلاعاتی در مورد ماتریس در اختیارمان می گذارد که در سیستم های معادلات خطی به درد می خورد. این عدد برای یافتن معکوس ماتریس و همچنین در معادلات دیفرانسیل و انتگرال و در شرایط بسیار دیگری به درد می خورد. اگر دترمینان ماتریسی مخالف صفر باشد، آنگاه در مییابیم که آن ماتریس معکوسپذیر است. از این رو از طریق دترمینان میتوان مقادیر ویژه یک ماتریس یا به عبارت بهتر یک نگاشت خطی از آن تعیین کرد. با استفاده از دترمینان میتوان معکوس ماتریسهای ۳×۳ و مراتب بالاتر را محاسبه کرد. حتی میتوان جهت حل معادله درجه ۳ از آنالیز ماتریسی و مفهوم دترمینان استفاده کرد.
ترانهاده ماتریس
ترانهاده، ابزاری است که در بدست آوردن ماتریس معکوس و بسیاری دیگر از مفاهیم جبر خطی کاربرد دارد. این ماتریس به دیگر ویژگیهای یک ماتریس همچون مربعی بودن، معکوسپذیر بودن و متقارن بودن آن وابسته است. یکی از کاربردهای مهم این مفهوم در تانسورها و در آنالیز برداری است. البته از این مفهوم برای ضرب دو بردار نیز استفاده میشود.
مثال: معکوس ماتریس 3*3 را محاسبه کنید. برای محاسبه انلاین معکوس ماتریس 3*3 کافی یکی از ماتریس ها را در سه سطر و سه ستون تنظیم کنیم و درایه ها را وارد کرده و روی گزینه معکوس ماتریس کلیک کنید و بلافاصله پاسخ نمایان خواهد شد.
بدست آوردن ماتریس ترانهاده
برای بدست آوردن ماتریس ترانهاده، میتوان به روشهای گوناگونی عمل کرد. توجه داشته باشید که هر ماتریسی با هر مرتبه و ویژگی را میتوان بهصورت ترانهاده بیان کرد. بهمنظور بدست آوردن ترانهاده بهترتیب زیر عمل کنید.
در ابتدا ماتریس A را بهصورت زیر در نظر بگیرید.
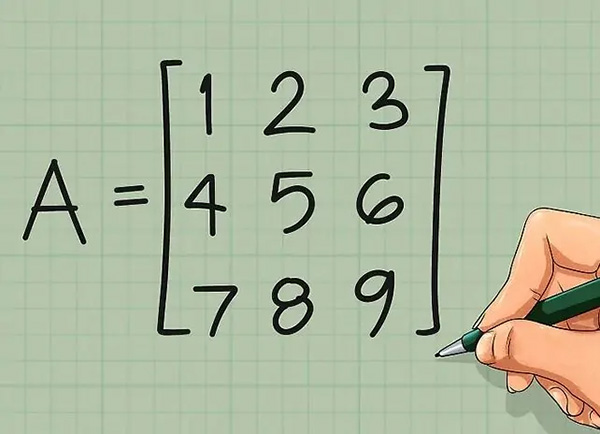
همانطور که میبینید بهمنظور راحتی کار ماتریس A بهصورت مربعی در نظر گرفته شده.
قدم اول
مطابق با تصویر زیر، سطر اول ماتریس A را در ستون اول قرار دهید.
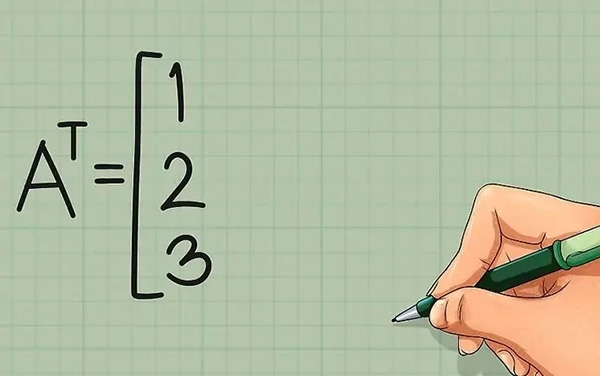
قدم دوم
همانطور که در شکل زیر نشان داده شده، قدم اول را برای دیگر سطرها نیز انجام دهید. نهایتا ماتریس AT، مطابق با تصویر زیر بدست میآید.
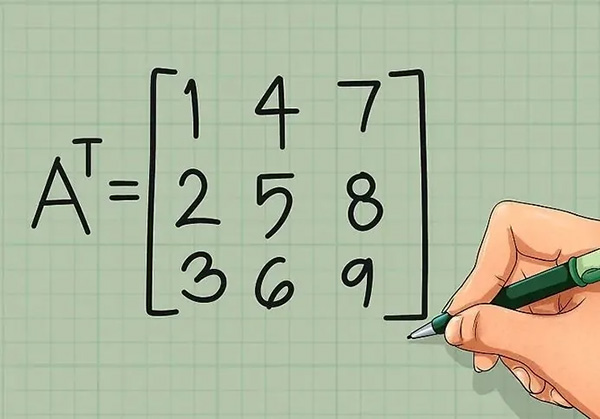
همانطور که در تصویر بالا نیز نشان داده شده، سطر دوم ماتریس A در ستون دوم ماتریس ترانهاده (AT)، نوشته شده است. به همین صورت سطر سوم در ستون سوم و الی آخر نوشته میشود.
با توجه به توضیحات بالا اعدادی که روی قطر ماتریس قرار میگیرند، ثابت میماند.
قدم سوم
همانطور که دیدید بدست آوردن ماتریس ترانهاده بسیار آسان بوده و حتی میتوان به صورت ذهنی آن را تصور کرد. اما در بسیاری از کاربردها، بایستی بتوانید شکل ریاضیاتی آن را نیز بیان کنید. در مورد ماتریس ترانهاده عبارات زیر را به خاطر بسپارید:
- اگر ماتریس B به صورت m×n باشد، آنگاه ماتریس BT، به شکل n×m در خواهد آمد.
- مولفه bij در ماتریس B برابر با مولفه bji در ماتریس BT است.
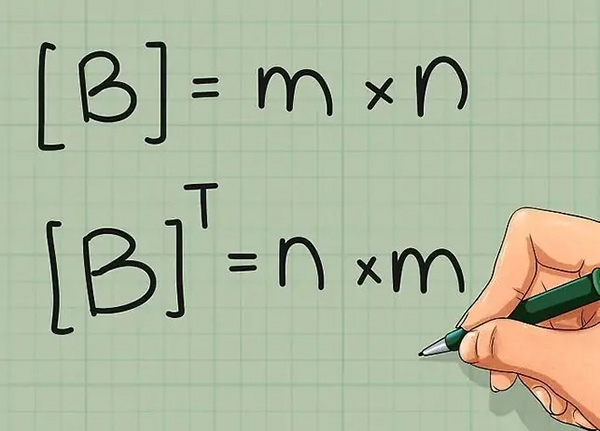
نکات
در ماتریس ترانهاده نکات مهمی نهفته است که بایستی آنها را فرا بگیرید.
MT)T=M)
برای هر ماتریس دلخواهی همچون M، رابطه MT)T=M) برقرار است. این رابطه میگوید ترانهادهی ترانهاده یک ماتریس برابر با خود ماتریس میشود.
قرینه ماتریس حول قطر اصلی
ممکن است زمان زیادی برای حل یک مسئله ریاضی نداشته باشید؛ بنابراین در چنین شرایطی بهمنظور بدست آوردن ترنهاده ماتریس میتوانید آن را حول قطر اصلیش قرینه کنید. در حقیقت مولفههای روی قطر اصلی را نگه داشته و بقیه اجزا را حول آن دوران دهید. برای نمونه در انیمیشن زیر نحوه بدست آمدن ماتریس ترانهاده نشان داده شده. همانطور که میبینید ماتریس A نسبت به محور اصلیش معکوس شده است.
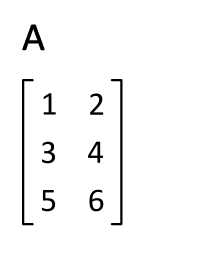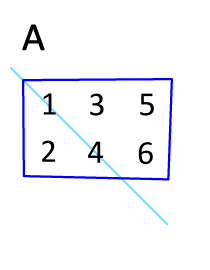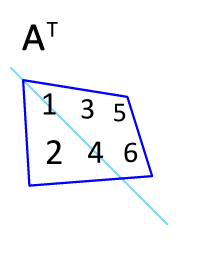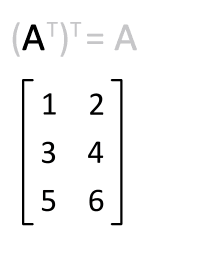
این روش خصوصا در مواردی که با ماتریسهای مربعی مواجه هستید، میتواند بسیار مفید باشد.
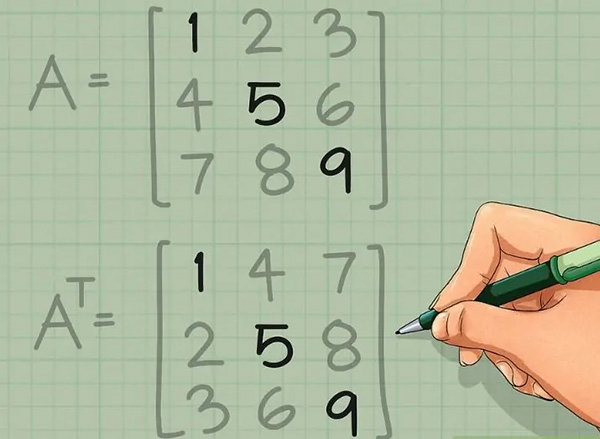
همانطور که در شکل فوق نیز میبینید مولفههای روی قطر اصلی ثابت نگه داشته شدهاند.
ماتریس متقارن
ماتریس متقارن، ماتریسی است که مولفههای آن نسبت به قطر اصلیش متقارن باشند. بدیهی است که ترانهاده چنین ماتریسی خودش میشود. بنابراین اگر A ماتریسی متقارن باشد، رابطه زیر را میتوان برای آن نوشت.
ترانهاد مزدوج
عدد مختلط، عددی است که از دو بخشِ حقیقی و موهومی تشکیل شده و میتوان آن را معادل با یک بردار فرض کرد.
اگر حتی یکی از مولفههای ماتریس، عددی مختلط باشد، آن ماتریس مختلط فرض میشود. برای نمونه ماتریس زیر نمونهای از یک ماتریس مختلط است.
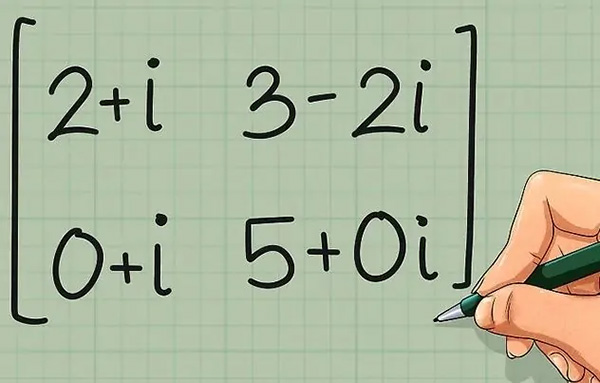
برای چنین ماتریسهایی میتوان ماتریسی تحت عنوان «ترانهاد مزدوج» (Conjugate Transpose) را تعریف کرد. بهمنظور یافتن چنین ماتریسهایی در ابتدا بایستی بخش موهومی هر درایه را قرینه کرده، سپس ترانهاده آن را نوشت. برای نمونه ماتریس فوق را در نظر بگیرید. بهمنظور نوشتن ترانهاده آن در ابتدا بخش موهومی هر مولفه را قرینه کنید (ماتریس زیر).
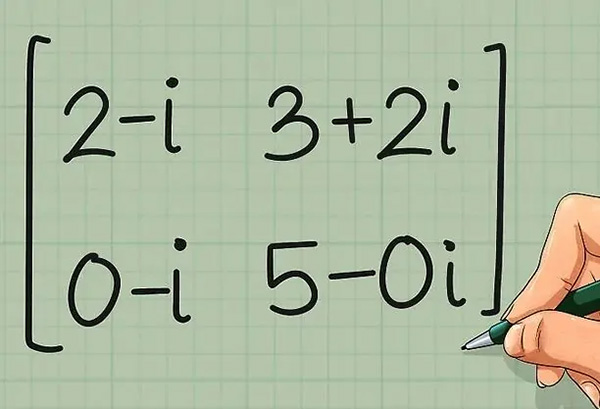
در مرحله بعد ترانهادهی ماتریس قرینه شده -در بالا- را مطابق با ماتریس زیر بنویسید.
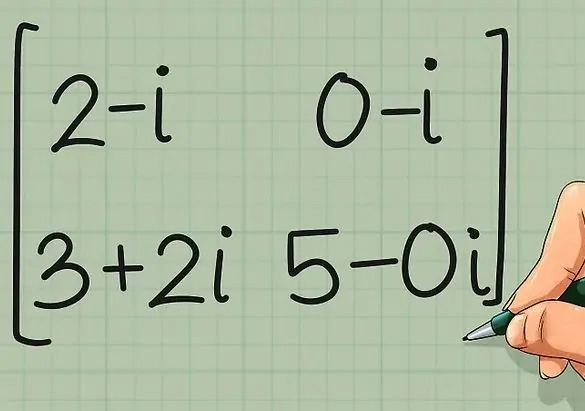
معمولا ماتریس ترانهاده مزدوج را با نماد H نمایش میدهند. بنابراین در مورد مثال فوق میتوان نوشت:
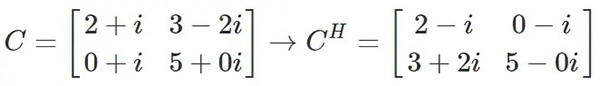
ویژگیهای ترانهاده
ماتریس ترانهاده دارای ویژگیهایی است که در اثبات قضایای ریاضی و فیزیک بسیار از آنها استفاده میشود. مهمترین ویژگیهای یک ماتریس ترانهاده به شرح زیر هستند:
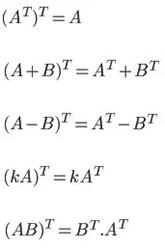
ویژگی آخر بیان شده ()، نکته جالبی را در خود دارد. در حقیقت اگر در این رابطه بهجای B، ماتریسِ AT قرار گیرد ، رابطه بدست میآید. بنابراین ترانهاده ماتریسِ برابر با خودش است. در حقیقت ماتریس متقارن است. از این نکته که حاصل ضرب یک ماتریس در ترانهادهاش، ماتریسی متقارن بوده، بسیار استفاده میشود.
منبع:فرادرس
